0. 前言
写完这篇文章后发现自己对于 DP 的优化一窍不通,所以补了补 DP 的一些优化,写篇 blog 总结一下。
1. 单调队列/单调栈优化
1.2 算法介绍
这应该算是最基础的 DP 优化方法了。
顾名思义,单调队列/单调栈优化 DP 就是保持容器内元素的单调性,以达成减少冗余状态的目的。
举单调队列的例子来说,当一个元素的两种属性(例如下标和权值)都优于另一元素时,就可以用此元素更换掉另一元素。这也正是 OI 界流传说法“当一个人比你小且比你强时,你就被弹出单调队列了”的原理。
我们以下面的例题作为例子来更具体地阐述这个算法。
1.3 适用范围&区别
一般来说,形如 \(f(i)=\max(f(j)+F(i)+F(j))\) 的式子都可以考虑适用单调队列/单调栈进行优化。(其中 \(F(i)\) 和 \(F(j)\) 表示和 \(i,j\) 有关的函数)
应该大部分人刚学这两种东西的时候都有一种疑惑:啥时候用单调队列,啥时候用单调栈呢?(至少我有
其实,它们两的本质区别还是其结构上的区别。单调栈通常用新加进来的东西替换掉一些栈顶元素,而单调队列是可能两端同时修改的。
在一下例题中我也会着重分析两者的使用。
1.4 例题
I. P1886 滑动窗口
这个不是优化 DP,就是最经典的裸的不能再裸的单调队列。
大力单调队列即可,时间复杂度 \(O(n)\)。
*II. CF372C Watching Fireworks is Fun
题目链接
OI Wili 推荐的题
题目大意:一个数轴上有 \(n\) 个点,每个点在位置 \(a_i\),有 \(m\) 个烟花要放,开始时间 \(t_i\)。你一开始的位置随便,每一单位时间可以最多走 \(d\) 这么多的距离,在 \(x\) 看到第 \(i\) 个烟花的快乐值为 \(b_i-|a_i-x|\),求最大的总代价。
数据范围:\(n\leq 150000,m\leq 300\)。
看到这个数据范围就知道大概是 \(O(nm)\) 的算法(最多要卡卡常)。
我们容易设计出 DP 状态 \(f(i,j)\) 表示放第 \(i\) 个烟花,位置在 \(j\) 时的最大快乐值。
转移:\(f(i,j)=\max_{j-(t_i-t_{i-1})\cdot d_i\leq k\leq j+(t_i-t_{i-1})\cdot d_i}(f(i-1,k)+b_i-|a_i-j|)\)。
接下来就需要对 DP 进行优化了,首先因为当 \(i\) 和 \(j\) 确定时 \(b_i-|a_i-j|\) 可以看做常数,剩下的就可以用单调队列去维护了。
注:本题使用单调队列的原因为 \(k\) 两边都有限制,需要头尾都更新。
时间复杂度 \(O(nm)\)。
III. P3572 [POI2014]PTA-Little Bird
IV. P1973 [NOI2011] NOI 嘉年华
V. P2254 [NOI2005] 瑰丽华尔兹
2. 斜率优化
斜率优化自己学过好几遍,也听 dalao 讲过,但是总是感觉半懂不懂的。这次索性把它给搞彻底了罢……
2.1 算法介绍
以 OI Wiki 上的例题为例。
题目大意:有 \(n\) 个玩具,每个玩具有一个价值 \(c_i\)。你需要将这 \(n\) 个玩具分成若干段,设一段 \([l,r]\) 的代价为 \((r-l+\sum_{i=l}^rc_i-L)^2\),其中 \(L\) 为常数,求最小的总代价。
数据范围:\(n\leq 5\times 10^4\)
使用 DP 优化的一般思路:先设计出一个超时的 DP 再优化。
设 \(f_i\) 表示前 \(i\) 个玩具的代价,那么得出转移方程为:
\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+\sum_{k=j+1}^ic_k+L)^2\} \]
用前缀和表示后即为:
\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+S_i-S_j+c_k+L)^2\} \]
其中 \(S_i=\sum_{k=1}^ic_k\)。
这就是朴素的 \(O(n^2)\) 的 DP。
下面就要优化了,不过有个问题:DP 跟斜率有什么关系呢?
考虑将 DP 转移方程转化为解析几何中直线的斜截式方程 \(y=kx+b\) 的形式。
我们先将只和 \(i,j\) 有关的归为一类,常数归为一类:\(a_i=s_i+i,b_i=s_i+i+L+1\),然后原式可以写成:
\[f_i=\min_{j=0}^{i-1}\{f_j+(a_i-b_j)^2\} \]
然后可以令 \(y=f_j+b_j^2,k=2a_i,x=b_j\)。(P.S. 这个应该只要满足 \(y=kx+b\) 都可以?)
此时需要最小化直线的截距,先将这些 \((x,y)\) 表示在平面直角坐标系中:
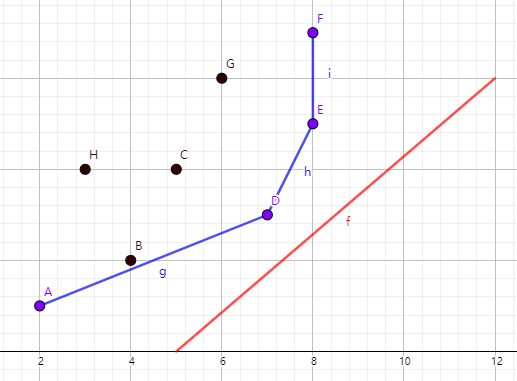
可以看到蓝线连成了一个下凸壳,第一个红线碰到的点使截距最小。
下面的问题就是怎样维护这个凸包,发现存在斜率递增,所以可以用单调队列来维护。
2.2 例题
I. P4072 [SDOI2016]征途
题目大意:有一个长度为 \(n\) 的序列 \((a_1,…,a_n)\),你要将它分成 \(m\) 段,求这 \(m\) 个和的最小方差。
数据范围:\(n\leq 3000,\sum a_i\leq 30000\)
这题是一道推柿子题。
设方差为 \(s\),则 \(s=\sqrt{\frac{(\bar{v}-v_1)^2+…+(\bar{v}-v_m)^2}{m}}\),然后愉快推柿子:
\[\begin{aligned} s^2 &=\frac{(\bar{v}-v_1)^2+…+(\bar{v}-v_m)^2}{m}\\ &=\frac{(\frac{\sum_{i=1}^mv_i}{m}-v_1)^2+…+(\frac{\sum_{i=1}^mv_i}{m}-v_m)^2}{m}\\ &=\frac{m\cdot(\frac{\sum_{i=1}^mv_i}{m})^2-2\cdot\frac{\sum_{i=1}^mv_i}{m}\cdot(v_1+…+v_m)+(v_1^2+…+v_m^2)}{m}\\ &=\frac{\frac{(\sum_{i=1}^mv_i)^2}{m}-2\cdot\frac{(\sum_{i=1}^mv_i)^2}{m}+\sum_{i=1}^mv_i^2}{m}\\ &=-\frac{\sum_{i=1}^mv_i}{m^2}+\frac{\sum_{i=1}^mv_i^2}{m} \end{aligned} \]
所以最后得到 \(s^2m^2=-\sum_{i=1}^mv_i+m\cdot\sum_{i=1}^mv_i^2\)。
II. Loj #10189 仓库建设
比较裸,一般转移方程很容易推:设 \(f(i)\) 表示在 \(1\text{~}i\) 中在 \(i\) 建设仓库的最小代价,则:
\[\begin{aligned} f(i) &=\min\{f_j+\sum_{k=j+1}^ip_k\cdot(x_i-x_k)\}\\ &=\min\{f_j+\sum_{k=j+1}^ip_kx_i-\sum_{k=j+1}^ip_kx_k\}\\ &=\min\{f_j+x_i\sum_{k=j+1}^ip_k-\sum_{k=j+1}^ip_kx_k\} \end{aligned} \]
设 \(S_i=\sum_{i=1}^ip_i,P_i=\sum_{i=1}^ip_ix_i\),则:
\[f(i)=\min\{f_j+x_i\cdot(P_i-P_j)-(S_i-S_j)+c_i\} \]
然后借用一个 dalao 的思考方式,当一个决策 \(j\) 优于一个决策 \(k\) 时,必有:
\[f_j+x_i\cdot(P_i-P_j)-(S_i-S_j)+c_i<f_k+x_i\cdot(P_i-P_k)-(S_i-S_k)+c_i\\ \]
即:
\[f_j-x_i\cdot P_j+S_j<f_k+x_i\cdot P_k+S_k\\ f_j-f_k+S_j-S_k<x_i\cdot(P_j+P_k)\\ \]
得到斜率形式:
\[\frac{(f_j+S_j)-(f_k+S_k)}{P_j+P_k}<x_i \]
这个直接冲斜率优化。
998244352. 参考资料
第 1 章:
第 2 章: