完全二叉树
完全二叉树的定义
满二叉树

非完全二叉树,非满二叉树
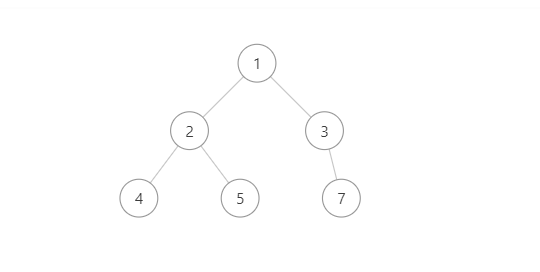
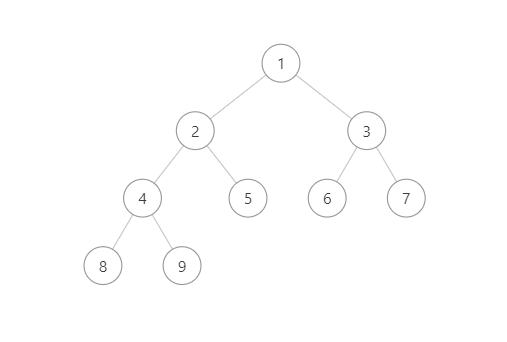
完全二叉树
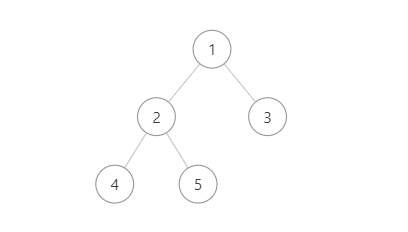
完全二叉树的特点
叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
完全二叉树的实现
- 二叉链表:直观,但占用内存大。
- 数组:简洁,但拓展麻烦。
比较推荐使用数组存储,本文也将基于数组存储介绍大顶堆的实现。
基于数组存储的完全二叉树节点与数组下标的关系
假设完全二叉树的 节点 A 存储在数组中的下标为 i
则:
节点 A的父节点存储在数组中的下标为(i - 1) / 2节点 A的左子节点存储在数组中的下标为2 * i + 1节点 A的右子节点存储在数组中的下标为2 * i + 2

堆
堆的定义
堆是一种特殊的数据结构,是高效的优先级队列,堆通常可以被看做一棵完全二叉树。
堆的分类
根据堆的特点,可以把堆分为两类:
- 大顶堆:每一个节点的值都大于或等于其左右子节点的值。
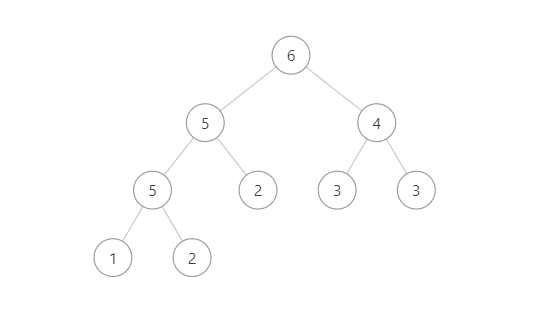
- 小顶堆:每一个节点的值都小于或等于其左右子节点的值。
堆的插入
往堆中插入数据,可能会破坏大顶堆(小顶堆)的性质,需要对堆进行调整。
堆的插入流程如下:
- 将插入的数据置于数组的尾部
- 将新插入的节点作为当前节点,比较当前节点与其父节点是否满足堆的性质,不满足则交换
- 重复步骤 2,直到满足堆的性质或者当前节点到达堆顶。
/**
* 添加元素
* @param value 待添加元素
*/
public void offer(int value){
if(this.currentLength >= this.capacity){ // 数组已耗尽,扩增数组为原来的两倍
this.grow();
}
int cur = this.currentLength++; // 获得待添加元素的添加位置
if(cur == 0){ // 当前堆为空直接添加
this.tree[cur] = value;
}else{ // 当前堆不为空,添加之后要向上调整
this.tree[cur] = value; // 步骤 1
int p = cur;
int parent = this.getParentIndex(p);
while(this.tree[parent] < this.tree[p]){ // 步骤 2
this.swap(parent, p);
p = parent;
parent = this.getParentIndex(p);
}
}
}
往堆中插入数据的时间复杂度为 O(logN)
堆的构建
构建一个大小为 N 的堆,其实就是执行 N 次插入。
所以构建一个大小为 N 的堆,其时间复杂度为 O(NlogN)
堆的删除
堆的删除也可能会破坏大顶堆(小顶堆)的性质,需要对堆进行调整。
堆的删除流程如下:
- 取出堆顶的数据
- 用堆的最后一个元素代替堆顶元素
- 判断当前节点(一开始是堆顶),是否满足大顶堆(小顶堆)的性质,不满足则用左右子节点中较大的节点进行交换
- 重复步骤 3 直到满足堆的性质或没有子节点
/**
* 取出最大元素
* @return 最大元素
*/
public int poll(){
if(isEmpty()){
throw new RuntimeException("堆为空,无法取出更多元素!");
}
int cur = --this.currentLength; // 获得当前堆尾
int result = this.tree[0]; // 取出最大元素 步骤1
this.tree[0] = this.tree[cur]; // 将堆尾移到堆头 步骤2
if(cur != 0){ // 如果取出的不是最后一个元素,需要向下调整堆 步骤3
int p = 0;
int left = getLeftIndex(p);
int right = getRightIndex(p);
// 由于是数组实现,数组元素无法擦除,需要通过边界进行判断堆的范围
// 当前节点和左节点在堆的范围内,
while(p < this.currentLength &&
0 <= left && left < this.currentLength &&
(this.tree[left] > this.tree[p] || this.tree[right] > this.tree[p])){
if(right >= this.currentLength){ // 当前节点没有右节点
if(this.tree[left] > this.tree[p] ){ // 左节点大于当前节点
swap(p, left);
p = left;
}
}else{ // 两个节点都在堆范围
if(this.tree[left] > this.tree[right]){ // 用大的节点替换
swap(p, left);
p = left;
}else{
swap(p, right);
p = right;
}
}
left = getLeftIndex(p);
right = getRightIndex(p);
}
}
return result;
}
堆的删除元素时间复杂度为 O(logN)
完整代码
// 大顶堆
public class Heap {
private int[] tree; // 数组实现的完全二叉树
private int capacity; // 容量
private int currentLength; // 当前数组已使用长度
/**
* 构造函数
* @param capacity 初始容量
*/
public Heap(int capacity) {
this.tree = new int[capacity];
this.capacity = capacity;
this.currentLength = 0;
}
/**
* 添加元素
* @param value 待添加元素
*/
public void offer(int value){
if(this.currentLength >= this.capacity){ // 数组已耗尽,扩增数组为原来的两倍
this.grow();
}
int cur = this.currentLength++; // 获得待添加元素的添加位置
if(cur == 0){ // 当前堆为空直接添加
this.tree[cur] = value;
}else{ // 当前堆不为空,添加之后要向上调整
this.tree[cur] = value; // 步骤 1
int p = cur;
int parent = this.getParentIndex(p);
while(this.tree[parent] < this.tree[p]){ // 步骤 2
this.swap(parent, p);
p = parent;
parent = this.getParentIndex(p);
}
}
}
/**
* 取出最大元素
* @return 最大元素
*/
public int poll(){
if(isEmpty()){
throw new RuntimeException("堆为空,无法取出更多元素!");
}
int cur = --this.currentLength; // 获得当前堆尾
int result = this.tree[0]; // 取出最大元素 步骤1
this.tree[0] = this.tree[cur]; // 将堆尾移到堆头 步骤2
if(cur != 0){ // 如果取出的不是最后一个元素,需要向下调整堆 步骤3
int p = 0;
int left = getLeftIndex(p);
int right = getRightIndex(p);
// 由于是数组实现,数组元素无法擦除,需要通过边界进行判断堆的范围
// 当前节点和左节点在堆的范围内,
while(p < this.currentLength &&
0 <= left && left < this.currentLength &&
(this.tree[left] > this.tree[p] || this.tree[right] > this.tree[p])){
if(right >= this.currentLength){ // 当前节点没有右节点
if(this.tree[left] > this.tree[p] ){ // 左节点大于当前节点
swap(p, left);
p = left;
}
}else{ // 两个节点都在堆范围
if(this.tree[left] > this.tree[right]){ // 用大的节点替换
swap(p, left);
p = left;
}else{
swap(p, right);
p = right;
}
}
left = getLeftIndex(p);
right = getRightIndex(p);
}
}
return result;
}
public boolean isEmpty(){
return this.currentLength <= 0;
}
private int getParentIndex(int index){
return (index - 1) / 2;
}
private int getLeftIndex(int index){
return 2 * index + 1;
}
private int getRightIndex(int index){
return 2 * index + 2;
}
private void swap(int left, int right){
int temp = this.tree[left];
this.tree[left] = this.tree[right];
this.tree[right] = temp;
}
/**
* 将数组拓展为原来的两倍
*/
private void grow(){
this.tree = Arrays.copyOf(this.tree, 2 * currentLength);
this.capacity = this.tree.length;
}
}
声明:本站所发布的一切破解补丁、注册机和注册信息及软件的解密分析文章仅限用于学习和研究目的;不得将上述内容用于商业或者非法用途,否则,一切后果请用户自负。本站信息来自网络,版权争议与本站无关。您必须在下载后的24个小时之内,从您的电脑中彻底删除上述内容。如果您喜欢该程序,请支持正版软件,购买注册,得到更好的正版服务。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。