总结以下刚做完的动态规划题集,题目和彩色图片均出自此题集。
规划问题就是在一定约束下寻找最优解,最优解是某种价值的最大(小)化,而这种价值一定是在某种变动之中累计的,这才需要规划,比如说青蛙跳台阶问题,一次可以跳一格,也可以跳两格;比如说礼物的最大价值问题,每次移动可以向左也可以向右;
这种变动总是可以描述为:物体从起始位置向其他位置移动 ,价值在经过任意位置时会发生改变,且移动过程中有若干路径可以选择。因此解决规划问题的关键就是寻找价值随着位置改变而改变的规律,从而选择最终价值最大的路径。
这种规律性被总结为动态规划的思想,我总结就是倒着想,正着解。
倒着想是指:
- 物体移动到最终位置前一步可以位于哪几个位置?
- 移动到这几个位置的最优解和移动到最终位置的最优解之间是否有函数关系f(x)?
- 物体从起始位置移动到哪些位置的路径是唯一的?
- 有唯一路径的位置的价值和从起点到其周边位置的最优解是否也满足函数关系f(x)?
如果二、四成立,则f(x)就是状态转移方程(状态定义为到达某一位置的最优解),三则是找到了我们可以依赖的起点,从起点经过状态转移方程就能找打到达任意位置的最优路径,这就是正着解。
我将我做过的动态规划问题总结为三类,总体做法是类似的,第一题详细讲倒着想,正着解的求解思路。
第一类动态规划问题——终点固定
1. 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
倒着想:
- 到达最右下角前有两步,其上方和其左侧
- 最右下角的上方和左侧的最优解和最终最优解的关系也很显然,两条路径的价值中大者即为到达最右下角的最优解
- 到达第一行、第一列的任意位置的路径是唯一的
- 第二条发现的规则显然是适用于到达任意位置的
因此,这道题可以很容易写出状态转移方程
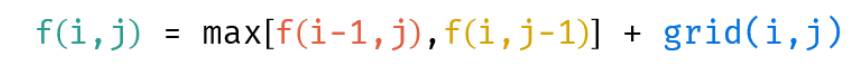
有了状态转移方程和初始状态,就可以正着解,也就是在第一行、第一列所有位置的最大价值已知的情况下,由状态转移方程依次计算出每行从左到右所有位置的最优解(这样就能保证每个位置求解时其上、右方位置最优解已被解出)。
<dir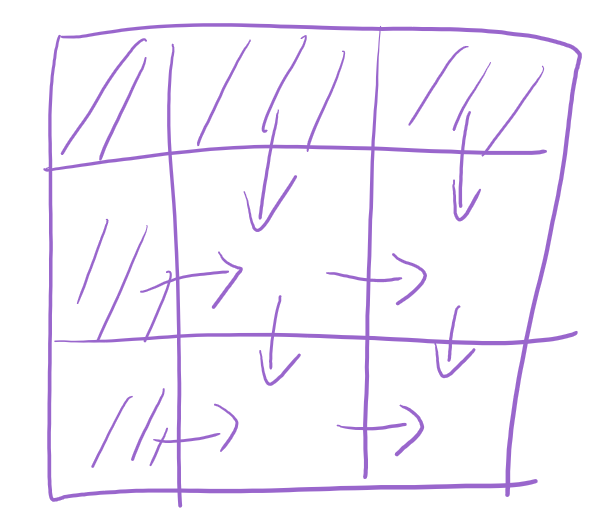
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
row_num = len(grid)
col_num = len(grid[0])
for i in range(row_num):
for j in range(col_num):
up = grid[i - 1][j] if i != 0 else 0
left = grid[i][j - 1] if j != 0 else 0
grid[i][j] = max(up, left) + grid[i][j]
return grid[row_num - 1][col_num - 1]
2. 青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
提示:
0 <= n <= 100
倒着想,很容易就写出状态转移方程

倒着想,实际是一种分治思想:假设输入n的解为F(n),利用分治思想,思考如果低规模问题解对于原问题是否有帮助,可以发现,如果F(n-1)和F(n-2)已知,F(n) = F(n-1) + F(n – 2),所以这是一个动态规划问题,已经写出状态转移方程
(注意:F(N-2)+1+1 和 F(n-1)+1是等价的,因为F(n-2)+1就是F(n-1)的一种跳法,这也是为什么不必考虑F(n-m)(m>1),因为这些从F(n-m)开始的跳法最终都将到达F(n-1)或F(n-2))
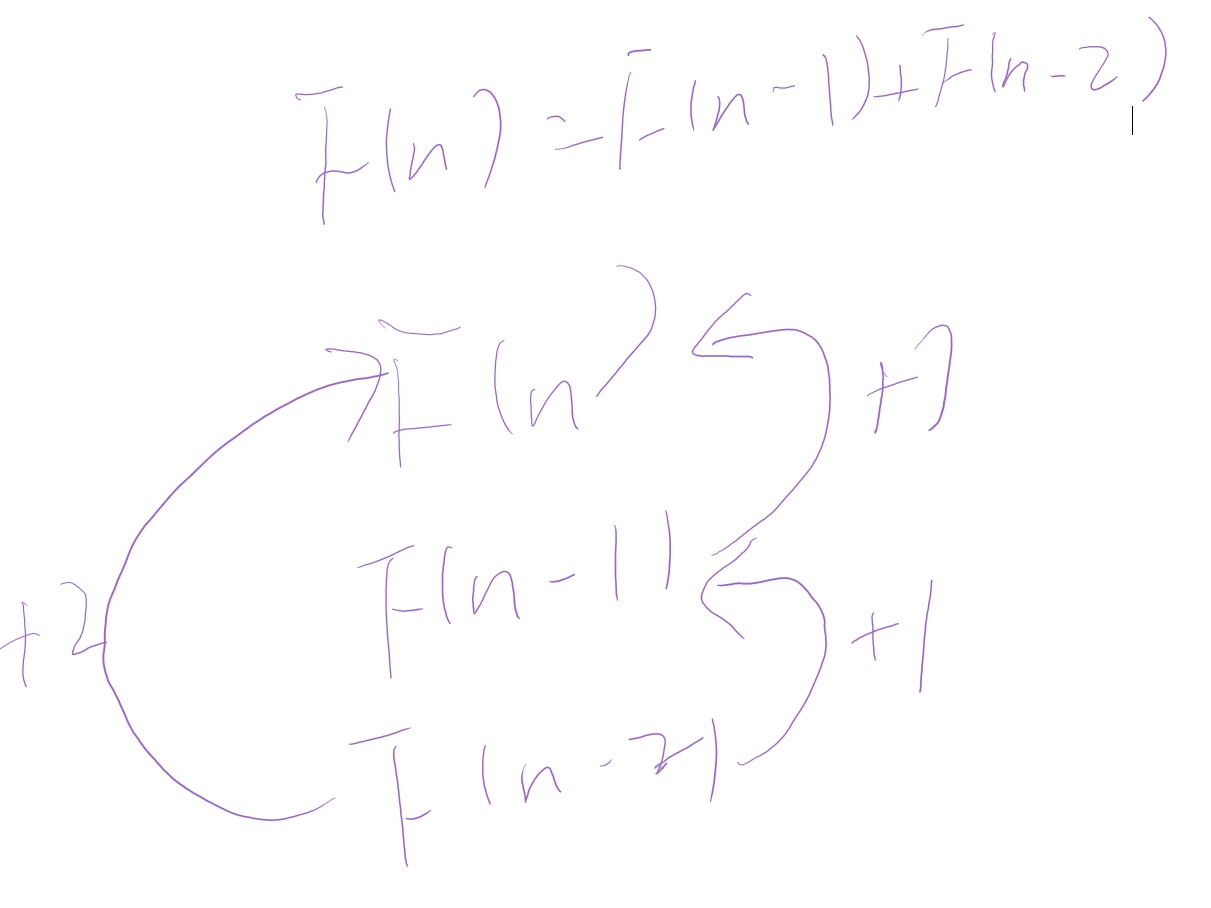
class Solution:
def numWays(self, n: int) -> int:
if n <= 1: return 1
c = 2
b = 1
a = int(1E9 + 7)
for i in range(n - 2):
c, b = (c + b) % a, c
return c
3. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

class Solution:
def translateNum(self, num: int) -> int:
s = str(num)
a = b = 1
for i in range(2, len(s) + 1):
a, b = (a + b if "10" <= s[i - 2:i] <= "25" else a), a
return a
4. n 个骰子的点数
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
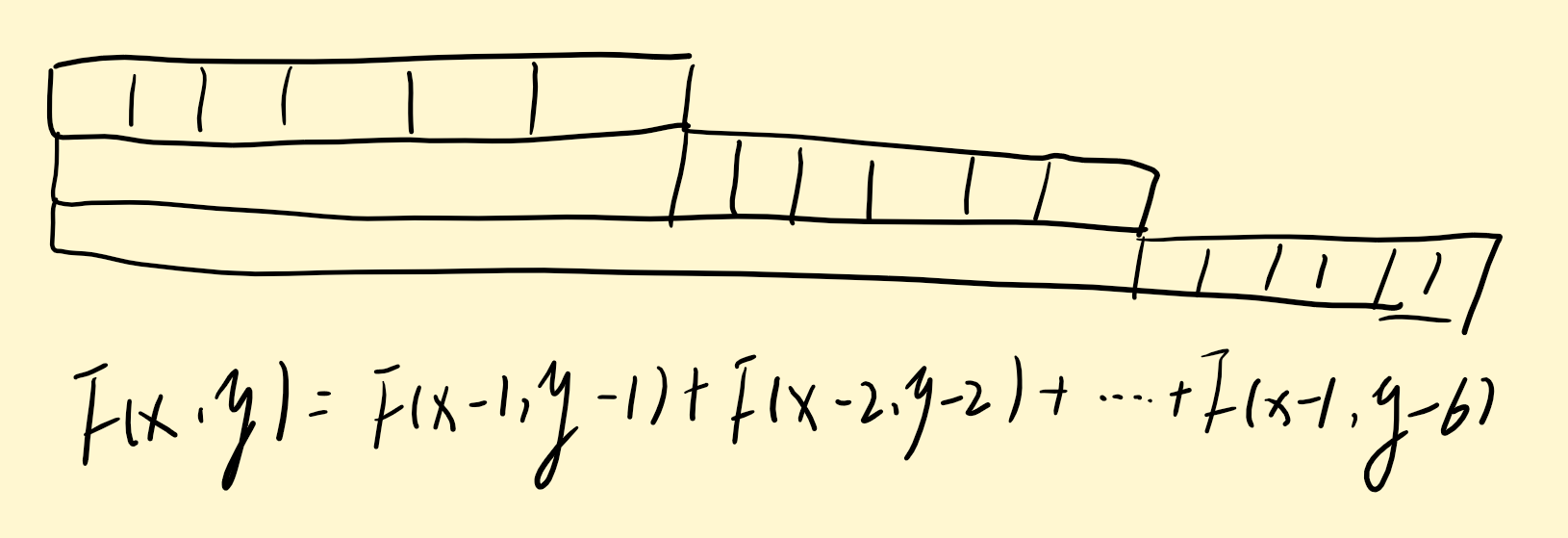
n个骰子总点数就有6*n种可能(其中前n种频次为0),n个骰子总点数为y有6种路径到达,当只有一个骰子时,到达任意点数的路径唯一,因此可以写出状态转移方程
class Solution:
def dicesProbability(self, n: int) -> List[float]:
dp = [1] * 6 # 存储少一个骰子的状态
for i in range(2, n + 1):
cur_num = i * 6 # 当有 i 个骰子的结果数
cur = [0] * cur_num # 当前骰子数的状态
for j in range(cur_num):
for m in range(1, 7):
exist = 0 <= j - m <= cur_num - 7
val = dp[j - m] if exist else 0
cur[j] += val
dp = cur
total = 6 ** n
return [x / total for x in dp][n - 1:]
第二类动态规划——终点不定
5. 连续子数组的最大和
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
这题和前面四个的差别在于,前面四个是从起点移动到固定重点的过程中某种价值累计的的最大值;而这道题中重点不是具体一个点,有几个点就有几个终点,最终求的是到达所有重点的价值之中最大值。
在这题中,最终解就是以任意数字结尾的最大子数组的和中的最大值。dp[i]代表以元素 nums[i]为结尾的连续子数组最大和
(状态不再是不同问题规模的原问题的解,而是不同问题规模下另一个问题的解,就是包含最后元素的子数组最大和的解,再由后者推出前者)
若dp[i−1]≤0 ,说明 dp[i – 1]对 dp[i]产生负贡献,即 dp[i-1] + nums[i]还不如 nums[i]本身大。
因此,状态转移方程为 dp[i] = nums[i] + max(dp[i], 0)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1, len(nums)):
nums[i] += max(nums[i - 1], 0)
return max(nums)
最开始分情况讨论,比较复杂

遇到正数就追加;更新子数组的转折点就是当前数组之和加上若干负数之后和≤0,因此遇到负数也直接追加。
这样,不管是正数和负数都直接追加,就保持了操作的统一,不需要真的去关心子数组的范围,只需要记录当前子数组的和以及出现过的最大子数组的和就可以。这样计算以每一个元素为结尾的最大子数组和就能和上面的动态规划解法一致。
第三类动态规划
6. 买股票的最佳时机
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
这题和上一题:连续子数组的最大和,的区别在于,虽然都是重点不定,但连续子数组的最大和问题中所有路径通过每个点价值都会产生变化,而这题不会,这题只有起点和终点价值会变化。
这题不用考虑路径上价值变化,回归最朴素的想法,每天价格-之前最低价,得到每天卖的获利,取最大即可
class Solution:
def maxProfit(self, prices: List[int]) -> int:
min_val = float('inf')
res = 0
for price in prices:
min_val = min(min_val, price) # 之前天最低股价
res = max(price - min_val, res)
return res