并查集学习知识点
·并查集概念
·并查集的基础操作:初始化、合并与查询
·并查集优化1:路径压缩
·并查集优化2:按秩合并(启发式合并)
·带权并查集
·种类并查集
引入:
话说在江湖中散落着各式各样的大侠,他们怀揣着各自的理想和信仰在江湖中奔波。或是追求武林至尊,或是远离红尘,或是居庙堂之高,或是处江湖之远。尽管大多数人都安分地在做自己,但总有些人会因为彼此的信仰不同而聚众斗殴。因此,江湖上常年乱作一团,纷纷扰扰。
这样长期的混战,难免会打错人,说不定一刀就把拥有和自己相同信仰的队友给杀了。这该如何是好呢?于是,那些有着相同信仰的人们便聚在一起,进而形成了各种各样的门派,比如我们所熟知的“华山派”、“峨嵋派”、“,崆峒派”、“少林寺”、“明教”……这样一来,那些有着相同信仰的人们便聚在一起成为了朋友。以后再遇到要打架的事时,就不会打错人了。
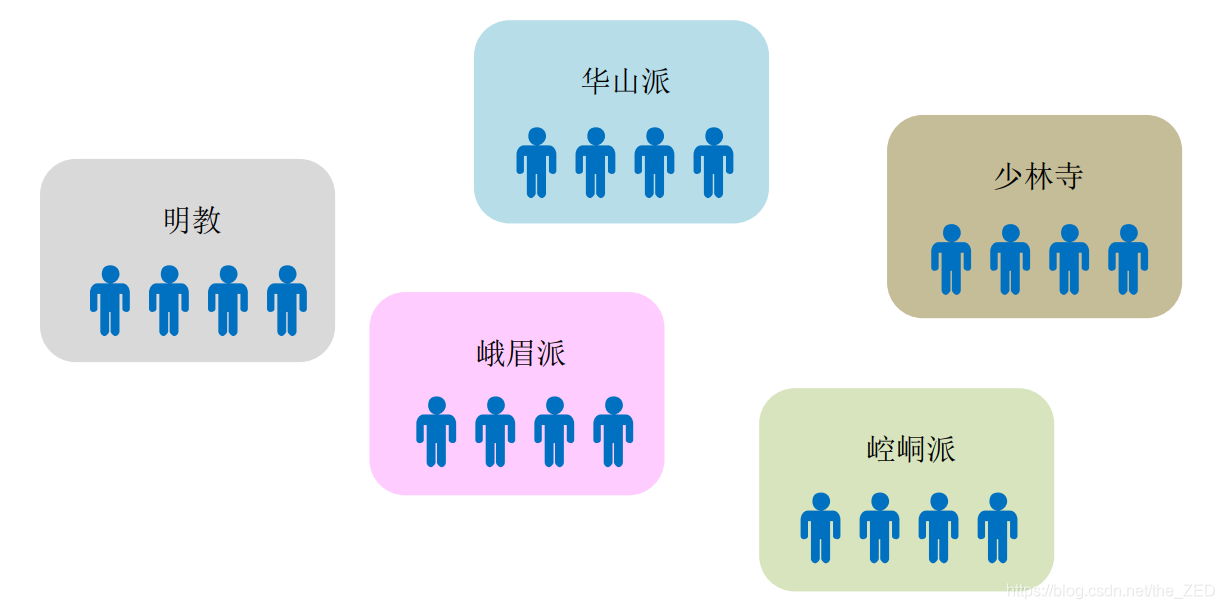
但是新的问题又来了,原本互不相识的两个人如何辨别是否共属同一门派呢?
这好办!我们可以先在门派中选举一个“大哥”作为话事人(也就是掌门人,或称教主等)。这样一来,每当要打架的时候,决斗双方先自报家门,说出自己所在门派的教主名称,如果名称相同,就说明是自己人,就不必自相残杀了,否则才能进行决斗。于是,教主下令将整个门派划分为三六九等,使得整个门派内部形成一个严格的等级制度(即树形结构)。教主就是根节点,下面分别是二级、三级、……、N级队员。每个人只需要记住自己的上级名称,以后遇到需要辨别敌友的情况时,只需要一层层往上询问就能知道是否是同道中人了。
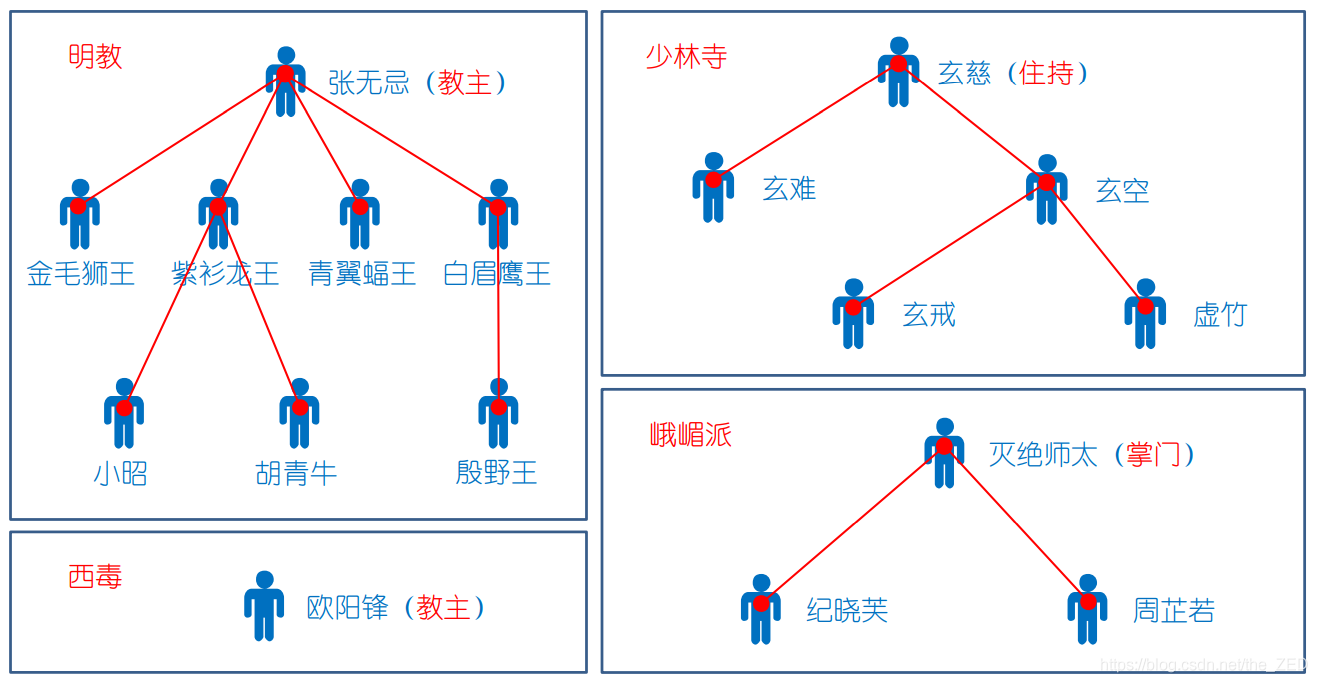
数据结构的角度来看:
由于我们的重点是在关注两个人是否连通,因此他们具体是如何连通的,内部结构是怎样的,甚至根节点是哪个(即教主是谁),都不重要。所以并查集在初始化时,教主可以随意选择(就不必再搞什么武林大会了),只要能分清敌友关系就行。
备注:上面所说的“教主”在教材中被称为“代表元”。
即:用集合中的某个元素来代表这个集合,则该元素称为此集合的代表元。
什么是并查集?
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内竞赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往超过了空间的限制,计算机无法承受;即使在空间上能勉强通过,运行的时间复杂度也极高,根本不可能在比赛规定的运行时间内计算出试题需要的结果,只能采用一种特殊数据结构——并查集来描述。
·举一个例子
设初始有若干元素:1,2,3,4,5,6,7,8
元素之间有若干关系:1~3,2~4,5~6,3~5,7~8,4~8
关系合并过程:
初始 {1},{2},{3},{4},{5},{6},{7},{8}
1~3:{1,3},{2},{4},{5},{6},{7},{8}
2~4:{1,3},{2,4},{5},{6},{7},{8}
5~6:{1,3},{2,4},{5,6},{7},{8}
3~5:{1,3,5,6},{2,4},{7},{8}
7~8:{1,3,5,6},{2,4},{7,8}
4~8:{1,3,5,6},{2,4,7,8}
并查集概念
并查集(Disjoint-Set或Union-Find Set)是一种表示不相交集合的数据结构,用于处理不相交集合的合并与查询问题。在不相交集合中,每个集合通过代表来区分,代表是集合中的某个成员,能够起到唯一标识该集合的作用。一般来说,选择哪一个元素作为代表是无关紧要的,关键是在进行查找操作时,得到的答案是一致的(通常把并查集数据结构构造成树形结构,根节点即为代表)。 在不相交集合上,需要经常进行如下操作:
·findSet(x):查找元素 x 属于哪个集合,如果 x 属于某一集合,则返回该集合的代表。
·unionSet(x,y):如果元素 x 和元素 y 分别属于不同的集合,则将两个集合合并,否则不做操作。
并查集的实现方法是使用有根树来表示集合——树中的每个结点都表示集合的一个元素,每棵树表示一个集合,每棵树的根结点作为该集合的代表。
并查集基础操作:初始化
现共有N个元素,对这N个元素要进行查询与合并操作,现进行初始化;例如N = 10,初始化方法如下,father[i]为i的父结点编号,初始化时结点的父结点为本身,即自己代表自己,建立N个独立集合:
void MakeSet(int n) {
for (int i = 1; i <= n; i++)
father[i] = i;
}并查集基础操作:查询
故事引入:
子夜,小昭于骊山下快马送信,发现一头戴竹笠之人立于前方,其形似黑蝠,倒挂于树前,甚惧,正系拔剑之时,只听四周悠悠传来:“如此夜深,姑凉竟敢擅闯明教,何不下坐陪我喝上一盅?”。小昭听闻,后觉此人乃明教四大护法之一的青翼蝠王韦一笑,答道:“在下小昭,乃紫衫龙王之女”。蝠王轻惕,急问道:“尔等既为龙王之女,故同为明教中人。敢问阁下教主大名,若非本教中人,于明教之地肆意走动那可是死罪!”。小昭吓得赶紧打了个电话问龙王:“龙王啊,咱教主叫啥名字来着?”,龙王答道:“吾教主乃张无忌也!”,小昭遂答蝠王:“张无忌!”。蝠王听后,抱拳请礼以让之。
在上面的情境中,小昭向他的上级(紫衫龙王)请示教主名称,龙王在得到申请后也向他的上级(张无忌)请示教主名称,此时由于张无忌就是教主,因此他直接反馈给龙王教主名称是“张无忌”。同理,青翼蝠王也经历了这一请示过程。
在并查集中,用于查询各自的教主名字的函数就是我们的find()函数。find(x)的作用是用于查找某个人所在门派的教主,换言之就是用于对某个给定的点x,返回其所属集合的代表。
实现:
首先我们需要定义一个数组:int pre[1000]; (数组长度依题意而定)。这个数组记录了每个人的上级是谁。这些人从0或1开始编号(依题意而定)。比如说pre[16]=6就表示16号的上级是6号。如果一个人的上级就是他自己,那说明他就是教主了,查找到此结束。也有孤家寡人自成一派的,比如欧阳锋,那么他的上级就是他自己。
每个人都只认自己的上级。比如小昭只知道自己的上级是紫衫龙王。教主是谁?不认识!要想知道自己教主的名称,只能一级级查上去。因此你可以视find(x)这个函数就是找教主用的。
查询操作是递归查询,在查询某个结点在哪一个集合中时,需沿着其父结点,递归向上,因所属集合代表指向的仍然是其本身,所以可以以father[x] == x作为递归查询出口。
int FindSet(int x) {
if (father[x] == x) return x;
else return FindSet(father[x]);
}例如要查询3所在的集合,只需要沿着3的父结点 向上,一直到一个自己指向自己的结点,该结点 就是这个3结点所属集合的代表,为2。
并查集基础操作:合并
故事引入:
虚竹和周芷若是我个人非常喜欢的两个人物,他们的教主分别是玄慈方丈和灭绝师太,但是显然这两个人属于不同门派,但是我又不想看到他们打架。于是,我就去问了下玄慈和灭绝:“你看你们俩都没头发,要不就做朋友吧”。他们俩看在我的面子上同意了,这一同意非同小可,它直接换来了少林和峨眉的永世和平。
实现:
在上面的情景中,两个已存的不同门派就这样完成了合并。这么重大的变化,要如何实现?要改动多少地方?其实很简单,我对玄慈方丈说:“大师,麻烦你把你的上级改为灭绝师太吧。这样一来,两派原先所有人员的教主就都变成了师太,于是下面的人们也就不会打起来了!反正我们关心的只是连通性,门派内部的结构不要紧的”。玄慈听后立刻就不乐意了:“凭什么是我变成她手下呀,怎么不反过来?我抗议!”。抗议无效,我安排的,最大。反正谁加入谁效果是一样的,我就随手指定了一个,Union()函数的作用就是用来实现这个的。
在进行集合的合并时,只需将两个集合的代表进行连接即可,即一个代表作为另一个代表的父结点。
Union(x,y)的执行逻辑如下:
1、寻找 x 的代表元(即教主);
2、寻找 y 的代表元(即教主);
3、如果 x 和 y 不相等,则随便选一个人作为另一个人的上级,如此一来就完成了 x 和 y 的合并。
下面给出这个函数的具体实现:
void UnionSet(int x, int y) {
father[FindSet(x)] = FindSet(y);
}
并查集优化1:路径压缩
问题引入:
前面介绍的 Union(x,y) 实际上为我们提供了一个将不同节点进行合并的方法。通常情况下,我们可以结合着循环来将给定的大量数据合并成为若干个更大的集合(即并查集)。但是问题也随之产生,我们来看这段代码:
if(fx != fy)
fa[fx]=fy; 这里并没有明确谁是谁的前驱(上级)的规则,而是我直接指定后面的数据作为前面数据的前驱(上级)。那么这样就导致了最终的树状结构无法预计,即有可能是良好的 n 叉树,也有可能是单支树结构(一字长蛇形)。试想,如果最后真的形成单支树结构,那么它的效率就会及其低下(树的深度过深,那么查询过程就必然耗时)。
而我们最理想的情况就是所有人的直接上级都是教主,这样一来整个树的结构就只有两级,此时查询教主只需要一次。因此,这就产生了路径压缩算法。
设想这样一个场景:两个互不相识的大将夏侯惇和许褚碰面了,他们都互相看不惯,想揍对方。于是按照江湖规矩,先打电话问自己的上级:“你是不是教主?” 上级说:“我不是呀,我的上级是***,我帮你问一下。” 就这样两个人一路问下去,直到最终发现他们的教主都是曹操。具体结构如下:
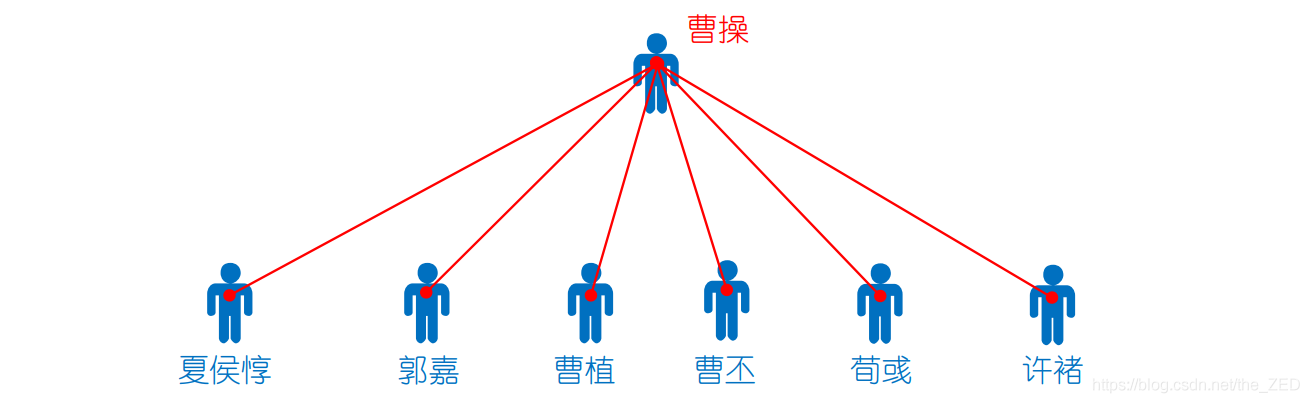
这样一来,在刚才查询过程中涉及到的人物就都聚集在了曹操的直接领导下,以后再需要查询教主名称的时候,就只需要询问一级便可得到。所以,在经过一次查询后,整个门派树的高度都将大大降低,路径压缩所实现的功能就是这么个意思。
对于一个集合中的结点,只需要关心它的根结点是谁,不必知道各结点之间的关系(对树的形态不关心),希望每个元素到根结点的路径尽可能短,最好只需要一步。把刚才的树转换为右图中的树,极大地提高了查询效率.路径压缩需要在查询操作时,把沿途的每个结点的父节点都设为根结点即可。下一次再查询时,就可以节约很多时间。
int FindSet(int x) {
if (father[x] == x) return x;
else return father[x] = FindSet(father[x]);
}
并查集优化2:按秩合并(启发式合并)
由于路径压缩只在查询时进行,每次查询也只压缩一条路径,所以并查集最终的结构仍然可能是比较复杂。例如,现在我们有一棵较复杂的树需要与一个单结点的集合合并。 如果把7的父节点设为8,会使树的深度加深,原来树中每个元素到根结点的距离都变长了。而把8的父结点设为7,则不会有这个问题,因为它没有影响到不相关的结点。
这启发我们:应该把深度低的树往深度高的树上合并,用rank数组记录根结点对应树的深度(如果不是根节点,其rank相当于以它作为根节点的子树的深度)。一开始,把所有元素的rank(秩)设为1。合并时比较两个根结点,把rank较小者往较大者上合并
//按秩合并初始化
void MakeSet(int n) {
for (int i = 1; i <= n; i++)
father[i] = i, rank[i] = 1;
}//按秩合并
void UnionSet(int x, int y) {
int a = FindSet(x), b = FindSet(y);
if (a == b) return;
if (rank[a] <= rank[b]) father[a] = b;
else father[b] = a;
if (rank[a] == rank[b]) rank[b]++;
}带权并查集(边带权并查集)
并查集实际上是若干棵树构成的森林,我们可以在树中的每条边上记录一个权值,即维护一个数组d,用d[x]保存节点x到父节点fa[x]之间的边权。在每次路径压缩后,每个访问过的节点都会直接指向树根,如果我们同时更新这些节点的d值,就可以利用路径压缩过程来统计每个节点到树根之间的路径上的一些信息。这就是所谓“边带权”的并查集。
eg.银河英雄传说
分析:一条“链”也是一棵树,只不过是树的特殊形态。因此可以把每一列战舰看作一个集合,用并查集维护。最初,N个战舰构成N个独立的集合。 在没有路径压缩的情况下,fa[x]就表示排在第x号战舰前面的那个战舰的编号。一个集合的代表就是位于最前边的那艘战舰。另外,让树上每条边权值为1,这样树上两点之间的距离减1就是二者之间间隔的战舰数量。
在考虑路径压缩的情况下,我们额外建立一个数组d,d[x]记录战舰x与fa[x]之间的边权。在路径压缩把x指向树根的同时,累加更新d[x],如下代码。
int Find(int x) {
if(x==fa[x]) return x;
int root=Find(fa[x]);
d[x]+=d[fa[x]];
return fa[x]=root;
}当接收到一个M x y指令时,把x的树根作为y的树根的子节点,连接在一起后,由于题意是x链接在y链后面(但实际形态不是链),所以y链中所有点p到fa[p]的边权不改变,而x链根节点rootx的边权要改变成y链中所有边数+1,即y链中所有节点数,最后y链的节点总数size[y]要累加x链的节点总数,代码如下。
fa[x]=y;
d[x]+=Size[y];
Size[y]+=Size[x];
Code
#include<bits/stdc++.h>
using namespace std;
int n,fa[30005],Size[30005],d[30005];
int read(){
int rv=0,fh=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') fh=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
rv=(rv<<1)+(rv<<3)+c-'0';
c=getchar();
}
return rv*fh;
}
int Find(int x)
{
if(x==fa[x])
return x;
int root=Find(fa[x]);
d[x]+=d[fa[x]];
return fa[x]=root;
}
int main()
{
for(int i=1;i<=30000;i++) {
fa[i]=i;
Size[i]=1;
d[i]=0;
}
char c;
int a,b,x,y;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf(" %c ",&c);
scanf("%d%d",&a,&b);
x=Find(a),y=Find(b);
if(c=='M')
{
fa[x]=y;
d[x]+=Size[y];
Size[y]+=Size[x];
}
else{
if(x!=y) printf("-1\n");
else {
if(a==b){
printf("0\n");
}
else{
printf("%d\n",abs(d[a]-d[b])-1);
}
}
}
}
return 0;
}种类并查集(扩展域并查集)
一般的并查集,维护的是具有连通性、传递性的关系,例如亲戚的亲戚是亲戚。但有时候要维护另一种关系:敌人的敌人是朋友。种类并查集就是为了解决这个问题。
我们开一个两倍大小的并查集。例如,假如我们要维护4个元素的并查集,我们改为开8个单位的空间,蓝色集合存储朋友关系,红色集合存储敌人关系,即5存储1元素的敌人关系,6存储2元素敌人关系…… 例如(1, 2)是敌人,(2, 4)是敌人.

eg.[BOI2003]团伙
Code
#include<bits/stdc++.h>
using namespace std;
int n,m;
int p[15000];
int vis[15000];
int find(int x){
if(x == p[x]) return x;
return p[x] = find(p[x]);
}
void un(int x, int y){
int xx = find(x);
int yy = find(y);
if(xx != yy) p[yy] = xx;
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1; i <= 2*n; i++)
p[i] = i;
for(int i = 1; i <= m; i++){
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
if(a == 0) un(b,c);
if(a == 1)
{
un(b+n,c);
un(b,c+n);
}
}
int cnt = 0;
for(int i = 1; i <= n; i++)
{
int t =find(i);
if(!vis[t])
{
vis[t] = 1;
cnt++;
}
}
printf("%d",cnt);
return 0;
}
参考:【算法与数据结构】—— 并查集